Java 에서 기본 배열 정렬 Arrays.sort() 는 Dual-Pivot Quicksort 알고리즘 즉 pivot 두 개를 사용해 배열을 세 구역으로 나누어 퀵정렬의 성능을 개선한 알고리즘을 사용하고 있습니다.
Collections.sort() 는 TimSort 알고리즘 즉 실제 데이터에서 효율적인 Merge Sort와 Insertion Sort의 하이브리드 알고리즘을 사용하고 있습니다.
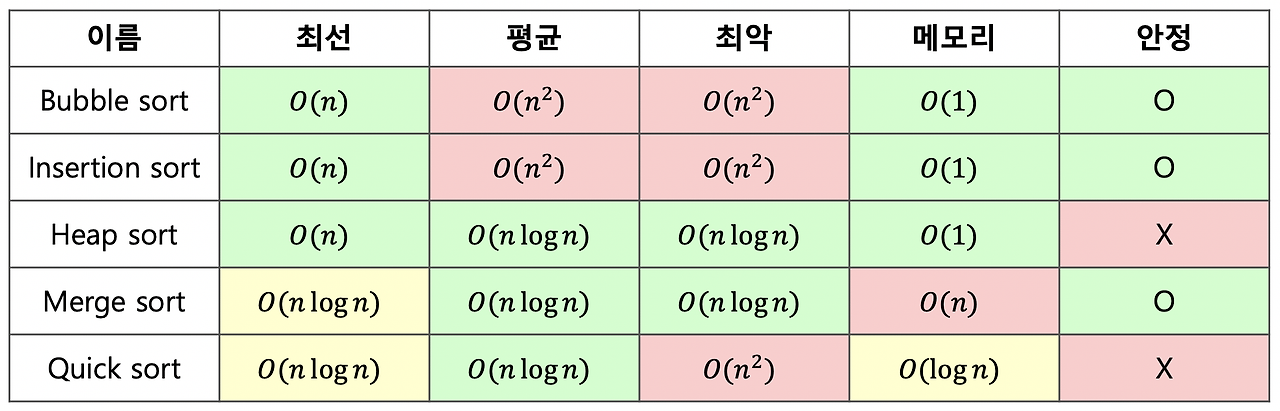
먼저 각 sort 방식에 대한 시간 복잡도를 따져보겠습니다.
1. Bubble Sort, Insertion Sort: O(n²) (느린 알고리즘)
이들 알고리즘은 배열 내에서 모든 요소를 비교하고 자리를 교환하는 방식으로 작동합니다.
Bubble Sort:
- 배열의 각 요소를 차례대로 비교하면서, 더 큰 값이 뒤로 가도록 교환합니다.
- 비교 횟수: 첫 번째 요소와 두 번째 요소를 비교하고, 그 다음 두 번째와 세 번째를 비교하는 식으로 반복합니다.
- 첫 번째 요소에 대해 n-1번 비교,
- 두 번째 요소에 대해 n-2번 비교,
- ... 마지막 요소까지.
- 즉, 비교 횟수는 약 n(n-1)/2에 해당하므로 O(n²)가 됩니다.
왜 n(n-1)/2 가 나오는가?
Bubble Sort를 예로 들어보면,
- Bubble Sort는 배열의 두 인접한 요소를 비교하면서, 더 큰 값을 오른쪽으로 이동시키는 방식입니다.
- 배열의 길이가 n일 때, 첫 번째 반복에서는 n-1번 비교합니다.
- 첫 번째 요소와 두 번째 요소를 비교하고, 두 번째 요소와 세 번째 요소를 비교하는 식으로, 마지막 요소 전까지 반복하므로 n-1번의 비교가 이루어집니다.
- 두 번째 반복에서는 이미 가장 큰 값이 정렬되어 있으므로 n-2번만 비교하면 됩니다.
- 이렇게 반복해서 마지막에는 비교할 값이 없을 때까지 비교가 줄어듭니다.
반복 횟수비교 횟수
| 첫 번째 반복 | n-1 |
| 두 번째 반복 | n-2 |
| 세 번째 반복 | n-3 |
| ... | ... |
| 마지막 반복 | 1 |
전체 비교 횟수 구하기
- 모든 반복에서의 비교 횟수를 더하면 총 비교 횟수는 다음과 같습니다.

- 이것이 O(n²) 로 나타나는 이유입니다. 왜냐하면 큰 수일수록 그 값은 n² 에 가까워지기 때문입니다.
Insertion Sort:
- 배열을 순차적으로 탐색하면서, 정렬된 부분과 정렬되지 않은 부분으로 나누고, 정렬되지 않은 부분의 첫 요소를 정렬된 부분의 적절한 위치에 삽입합니다.
- 비교 횟수: 최악의 경우 모든 요소를 모두 비교하고 위치를 찾아야 하므로 n(n-1)/2 번 비교, 즉 O(n²) 가 됩니다.

https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html
결론적으로, 이 두 알고리즘은 데이터의 크기가 커질수록 비교해야 할 횟수가 급격히 증가하므로 느린 알고리즘으로 간주됩니다.
2. Merge Sort, Quick Sort, Heap Sort: O(n log n) (빠른 알고리즘)
이들 알고리즘은 분할 정복 또는 특정 자료구조를 사용해 비교 횟수를 줄이는 방식으로 동작합니다.
Merge Sort:
- 배열을 반으로 나누고 (Divide), 각 반을 재귀적으로 정렬한 후, 두 부분을 병합하여 정렬된 배열을 만듭니다 (Conquer).
- 배열을 log n번 나누고, 각 단계에서 두 부분을 병합하는 데 O(n) 시간이 걸리므로, 전체 시간 복잡도는 O(n log n) 입니다.
Quick Sort:
- 배열에서 하나의 기준 값을 선택(피벗)하고, 이를 기준으로 작은 값과 큰 값으로 나눕니다. 그런 다음 두 부분을 재귀적으로 정렬합니다.
- 평균적으로 배열을 나누는 데 log n단계가 필요하고, 각 단계에서 배열을 분할하는 데 O(n) 시간이 걸립니다.
- 따라서 평균 시간 복잡도는 O(n log n) 입니다.
Heap Sort:
- Heap 이라는 자료구조를 사용하여 정렬을 수행합니다. Heap 을 구성하는 데 O(log n) 시간이 걸리며, 최대 또는 최소값을 제거하는 데도 O(log n) 시간이 걸립니다.
- 전체적으로 n번 삽입과 제거를 반복하므로 O(n log n) 입니다.
느린 알고리즘 vs 빠른 알고리즘
- O(n²): 두 요소를 비교하는 횟수가 배열의 크기에 비례적으로 늘어납니다.
- 배열이 커지면, 비교 횟수가 급격히 증가해 성능이 떨어집니다.
- 예를 들어, 10개의 데이터를 정렬할 때는 100번의 비교가 필요하지만, 100개의 데이터를 정렬하려면 10,000번의 비교가 필요합니다.
- O(n log n): 배열을 재귀적으로 나누어 비교 횟수를 줄이는 방식입니다.
- 배열을 나눌수록 비교 횟수는 줄어들기 때문에, 데이터가 커지더라도 비교 횟수는 상대적으로 적게 증가합니다.
- 예를 들어, 100개의 데이터를 정렬할 때 n log n은 약 700번의 비교가 필요합니다. (100 * log₂100 ≈ 100 * 7)
정리
- O(n²) 알고리즘은 데이터 크기가 커질수록 비교 횟수가 급격히 증가하여 느려집니다.
- O(n log n) 알고리즘은 데이터 크기가 커져도 상대적으로 적은 비교를 필요로 하기 때문에 더 빠른 성능을 보입니다.
그리고 한가지 더 의문이 들었던 점은 Heap sort 만이 가지는 장점은 뭘까? 였습니다.
왜냐하면 트리 기반의 구조로 각 노드가 부모-자식 관계로 연결되어 있겠지만,
실제 메모리 상에서는 트리의 각 노드가 항상 연속적인 메모리 블록에 위치하지 않을텐데
그럼 노드를 방문할때마다 멀리 떨어진 메모리 주소로 가야하지 않을까 ,, 라는 생각이 들었기 때문입니다.
그러다 Tim Sort 관련 아티클에 참조 지역성 이라는 키워드로 해당 부분을 게시한 부분을 발견했습니다.
시간 복잡도가 O(nlogn) 이라는 말은 실제 동작 시간은 C × nlogn + α라는 의미이다.
상대적으로 무시할 수 있는 부분인 부분을 제하면 에는 앞에 라는 상수가 곱해져 있어 이 값에 따라 실제 동작 시간에 큰 차이가 생긴다.
이 라는 값에 큰 영향을 끼치는 요소로 '알고리즘이 참조 지역성(Locality of reference) 원리를 얼마나 잘 만족하는가' 가 있다.
참조 지역성 원리 란, CPU가 미래에 원하는 데이터를 예측하여 속도가 빠른 장치인 캐시 메모리에 담아 놓는데 이때의 예측률을 높이기 위하여 사용하는 원리이다.
쉽게 말하자면, 최근에 참조한 메모리나 그 메모리와 인접한 메모리를 다시 참조할 확률이 높다는 이론을 기반으로 캐시 메모리에 담아놓는 것이다.
메모리를 연속으로 읽는 작업은 캐시 메모리에서 읽어오기에 빠른 반면, 무작위로 읽는 작업은 메인 메모리에서 읽어오기에 속도의 차이가 있다.
reference < https://d2.naver.com/helloworld/0315536 >
Quick Sort의 평균 O(n log n) vs. 최악 O(n²)
- 평균적인 경우: Pivot 이 배열을 균등하게 나누면,
- 각 재귀 호출마다 배열을 반으로 나누는 작업이 이루어지므로 O(log n) 번 재귀 호출이 발생합니다.
- 그리고 각 호출마다 배열을 순회하면서 분할 작업이 이루어지므로 O(n) 의 시간이 걸립니다. 이 경우 평균 시간 복잡도는 O(n log n)입니다.
- 최악의 경우: Pivot 이 항상 배열의 가장 작은 값이나 가장 큰 값으로 선택되면, 배열이 불균형하게 나누어집니다.
- 이 경우 pivot 으로 인해 한쪽 배열만 남고, 매번 거의 전체 배열을 다시 순회해야 하므로, 전체 시간 복잡도는 O(n²)이 됩니다.
- 배열: [1, 2, 3, 4, 5, 6, 7]
1단계: 피벗으로 7 선택 → [1, 2, 3, 4, 5, 6] | 7
2단계: 피벗으로 6 선택 → [1, 2, 3, 4, 5] | 6 | 7
3단계: 피벗으로 5 선택 → [1, 2, 3, 4] | 5 | 6 | 7
... - 이 경우 매번 배열을 하나씩만 줄이면서 전체 배열을 순회해야 하므로, O(n²) 시간이 걸리게 됩니다.
Heap Sort는 항상 O(n logn) 시간 복잡도라는 장점 vs. 참조 지역성 관련 단점
- Heap Sort가 항상 O(n log n)인 이유
- Heap Sort는 우선 배열을 힙(Heap) 자료구조로 변환한 뒤, 최대값(또는 최소값)을 하나씩 꺼내 배열 끝으로 옮기면서 정렬을 진행합니다.
- 힙 구성 (Build Heap): O(n)
- 주어진 배열을 Heap 으로 변환하는 과정에서는 배열을 Tree 형태로 재구성합니다.
- 이때 Tree 의 각 Node 에서 자식 Node 들과 비교하면서 Heap 속성을 만족하도록 만들어야 합니다.
- Heap 구성 자체는 O(n)의 시간이 걸립니다.
- 힙 정렬 (Heapify + Extract): O(n log n)
- Heap 에서 최대값을 꺼내는 과정은 Tree 의 root(최대값 또는 최소값)에서 값을 꺼낸 뒤, 다시 tree 를 재구성해야 합니다.
- 이때 트리의 높이가 log₂(n) 이기 때문에 최대값을 꺼내고 나머지 트리를 재구성하는 과정은 O(log n)의 시간이 걸립니다.
- 이 과정을 n번 반복해야 하므로 전체 시간 복잡도는 O(n log n)이 됩니다.
- 배열: [7, 4, 8, 3, 9, 1, 2]
1단계: 배열을 힙으로 변환 (최대 힙)
[9, 7, 8, 3, 4, 1, 2]
2단계: 최대값 9를 꺼내 배열 끝으로 옮기고 나머지 힙을 재구성 (8, 7, 4, ...)
- Heap 에서 최대값을 꺼내는 과정은 Tree 의 root(최대값 또는 최소값)에서 값을 꺼낸 뒤, 다시 tree 를 재구성해야 합니다.
Heap Sort는 항상 Tree 기반이므로 최악의 경우에도 Tree 의 깊이에 비례하는 O(log n)의 작업을 n번 반복하게 됩니다.
따라서 항상 O(n log n) 의 시간이 걸립니다.
하지만 단점도 있는데요.
Heap sort 의 경우 대표적으로 참조 지역성이 좋지 않은 정렬이라고 합니다.
위의 이미지에서 확인할 수 있듯이
한 위치에 있는 요소를 해당 요소의 인덱스 두 배 또는 절반인 요소와 반복적으로 비교하기에
캐시 메모리에서는 예측하기가 매우 어렵습니다.
그렇기에 C × nlogn + α 에서 C 가 상대적으로 Quick Sort, Merge Sort 보다 큰 값으로 정의된다는 단점입니다.
위에서 정렬 알고리즘의 장단점을 살펴보았는데요.
이런 장단점을 보완해 Insertion sort와 Merge sort를 결합하여 2002년 소프트웨어 엔지니어 Tim Peters에 의하여
Tim Sort 라는 정렬 알고리즘이 등장했다고 합니다.
실생활 데이터의 특성을 고려하여 더욱 빠르게 고안된 이 알고리즘은
최선의 시간 복잡도는 , 평균은 O(nlogn), 최악의 경우 시간 복잡도는
Tim sort는 안정적인 두 정렬 방법을 결합했기에 안정적이며,
추가 메모리는 사용하지만 기존의 Merge sort에 비해 적은 추가 메모리를 사용하여
다른 O(nlogn) 정렬 알고리즘의 단점을 최대한 극복한 알고리즘이라고 합니다.


1. ∣C∣>∣A∣+∣B∣
2. ∣B∣>∣A∣
Tim Sort 에서 배열 merge 과정에서 위의 조건을 만족하지 않을 경우 B는 와 중 작은 run과 병합한다고 하는데
이는 에서 인접한 두 run을 모두 확인하여 그 중 가장 비슷한 run과 병합하여 최소한의 메모리로 효율을 내는 방식과,
One Pair at a Time Mode로 두 개의 Run(A와 B)의 현재 원소를 하나씩 비교하며 run 의 포인터를 이동시키다가
A에서 원소가 계속 오름차순이면 Galloping mode 로 연속적인 오름차순을 감지해서 1개, 2개, 4개, 8개 등의 원소를 한 번에 비교하면서 더 빠르게 병합할 수 있다는게 인상 깊었습니다 !
'java' 카테고리의 다른 글
| Java 시간 유형에 대한 고민 (1) | 2024.04.19 |
|---|---|
| HashMap 의 동작 원리 (1) | 2024.02.27 |
| method class instance object (0) | 2022.09.23 |
| 생성자 내부클래스 (1) | 2022.09.23 |
| Linked List vs Array List (0) | 2022.09.23 |



